This Pascal program finds the value of a Nth order polynomial:
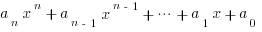
implementing Horner method without using any complex arithmetic in Fortran 77.
Obviously, it can find complex values, for complex x’s, but without complex arithmetic.
The program also uses ANSI codes to clear screen.
PROGRAM HORNER1 REAL A(0:30),B(0:30),K,L,IM,R,AT,BT,PR,PIM INTEGER N,I CHARACTER ESC ESC=CHAR(27) CALL CLS() WRITE (*,*) 'PLEASE, ENTER THE CLASS N OF THE POLYNOMIAL:' READ (*,*) N WRITE (*,*) 'ENTER a0,a1,a2,a3...aN' C READ (*,*) (A(I),I=0,N) DO 5 I=0,N READ(*,*) A(I) 5 CONTINUE C x1= a+bi where a=R AND b=IM WRITE (*,*) 'TYPE THE REAL AND THE IMAGINARY PARTS OF X1:' READ (*,*) R,IM WRITE (*,*) 'CALCULATING....' C x^2-2ax+a^2+b^2 C P(x)=(x^2-kx-lx)P2(x) + Ax+B C k=2a l=-^2-b^2 K=2*R L=-R^2-IM^2 WRITE (*,*) 'K,L are:' , K,L C HORNER ROUTINE: C Bn=An, Bn-1=An-1 + kBn, Bk-2=Ak-2 + kBk-1 + l Bk ,k=n,...2 C A=B1 , B=B0 C P(x1)=Ax1 + B B(N)=A(N) B(N-1)=A(N-1)+K*B(N) WRITE (*,*) '....CALCULATING....' DO 10 I=N,2,-1 B(I-2)=A(I-2)+K*B(I-1)+L*B(I) 10 CONTINUE C A=B1 C B=B0-kB1 AT=B(1) BT=B(0)-K*B(1) CALL CLS() WRITE(*,*) 'A,B=',AT,BT C P(x1)=AX1 + B PR=AT*R+BT PIM=AT*IM WRITE (*,20) ESC,PR,PIM 20 FORMAT(1X,A,'[10;3f','The value of P=','(',F8.3,',',F8.3,')') STOP END SUBROUTINE CLS () CHARACTER ESC ESC= CHAR(27) WRITE (*,100) ESC 100 FORMAT(1X,A,'[2J') WRITE (*,*) 'N-R HORNER METHOD -- VALUE OF CLASS N POLYNOMIAL B WITHOUT COMPLEX ARITHMETIC' RETURN END |






Leave a Reply