This program uses the basis of the Archimedes (287-212 BC) method, known as exhaustion, to approximate the integral of a given real function in a given space [a,b]. First it segments the given space into N subspaces. It calculates: a) the sum of the areas of orthogonal parallelograms of height equal to the minimum of the function in each segment and b) the sum of the areas of orthog. parallelograms of height equal to the max value of f(x) in each segment. Theoretically, when 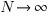 , the progressions are both converging to the same limit which is the integral of the function.
, the progressions are both converging to the same limit which is the integral of the function.
The program is simple. It requires the segmentation number N and the integration limits a,b. You can easily change the function to your desired one in the function at the end of the code. As you may see, after the calculations, it tries to graph the function. Well don’t expect much, although it has very good output in some functions like the f(x)=xsinx.
The program was written in Borland C++ 5.0. You will need the compiler bcc in order to compile and run it, but it’s very easy to make some alterations for other compilers or other OS’s.





